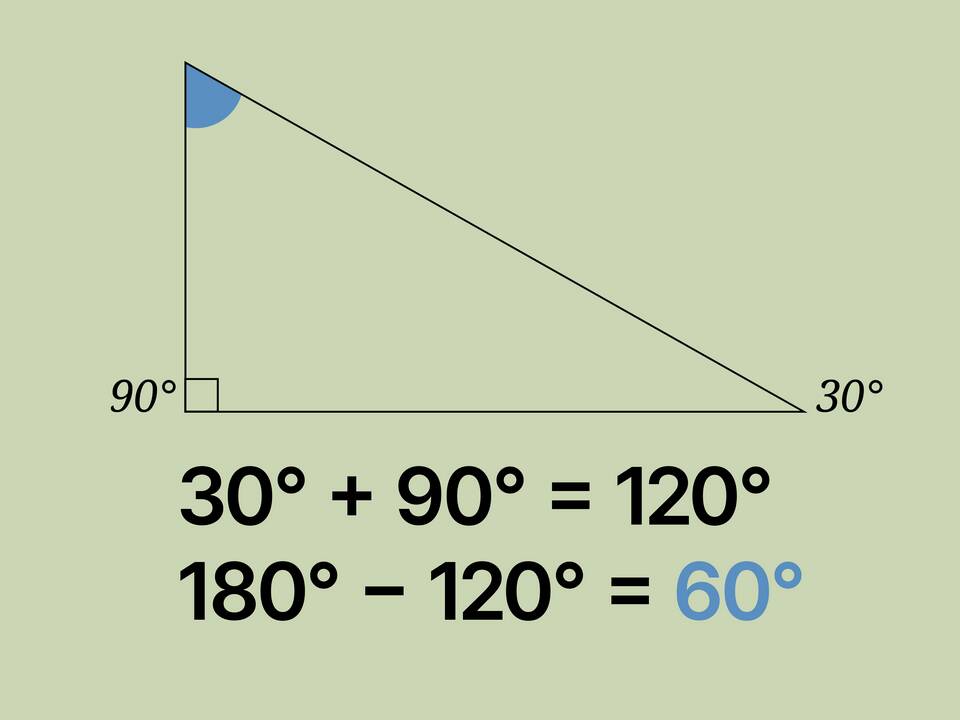
Сумма углов треугольника - это фундаментальное понятие в геометрии, которое устанавливает важную зависимость между углами любой треугольной фигуры. Данное свойство активно используется при решении геометрических задач и доказательстве теорем.
Содержание
Основная теорема о сумме углов
В евклидовой геометрии сумма внутренних углов любого треугольника всегда равна 180 градусам (или π радианам). Это можно выразить формулой:
∠A + ∠B + ∠C = 180°
где ∠A, ∠B и ∠C - внутренние углы треугольника.
Доказательство теоремы
Рассмотрим классическое доказательство через параллельные прямые:
- Проведем через вершину B прямую, параллельную стороне AC
- Образовавшиеся углы при точке B будут равны углам A и C как накрест лежащие
- Три угла при точке B составляют развернутый угол, равный 180°
- Следовательно, сумма углов треугольника ABC равна 180°
Примеры вычислений
| Тип треугольника | Пример вычисления суммы углов |
| Равносторонний | 60° + 60° + 60° = 180° |
| Прямоугольный | 90° + 45° + 45° = 180° |
| Тупоугольный | 120° + 30° + 30° = 180° |
Исключения и особые случаи
В неевклидовых геометриях сумма углов треугольника может отличаться:
- В сферической геометрии сумма углов всегда больше 180°
- В геометрии Лобачевского сумма углов всегда меньше 180°
- Для вырожденного треугольника (с нулевой площадью) сумма углов может быть меньше 180°
Практическое применение
Знание суммы углов треугольника позволяет:
- Находить неизвестные углы в треугольнике
- Доказывать равенство или подобие треугольников
- Решать задачи на построение
- Вычислять углы в многоугольниках через разбиение на треугольники
Заключение
Теорема о сумме углов треугольника является одной из базовых в геометрии. Понимание этого принципа открывает возможности для решения широкого круга геометрических задач как в теории, так и на практике.